Next: Midi/Frequency Conversion Up: Discrete-Time Signals, Amplitude and Frequency Previous: Exponential Decay and Time Constants
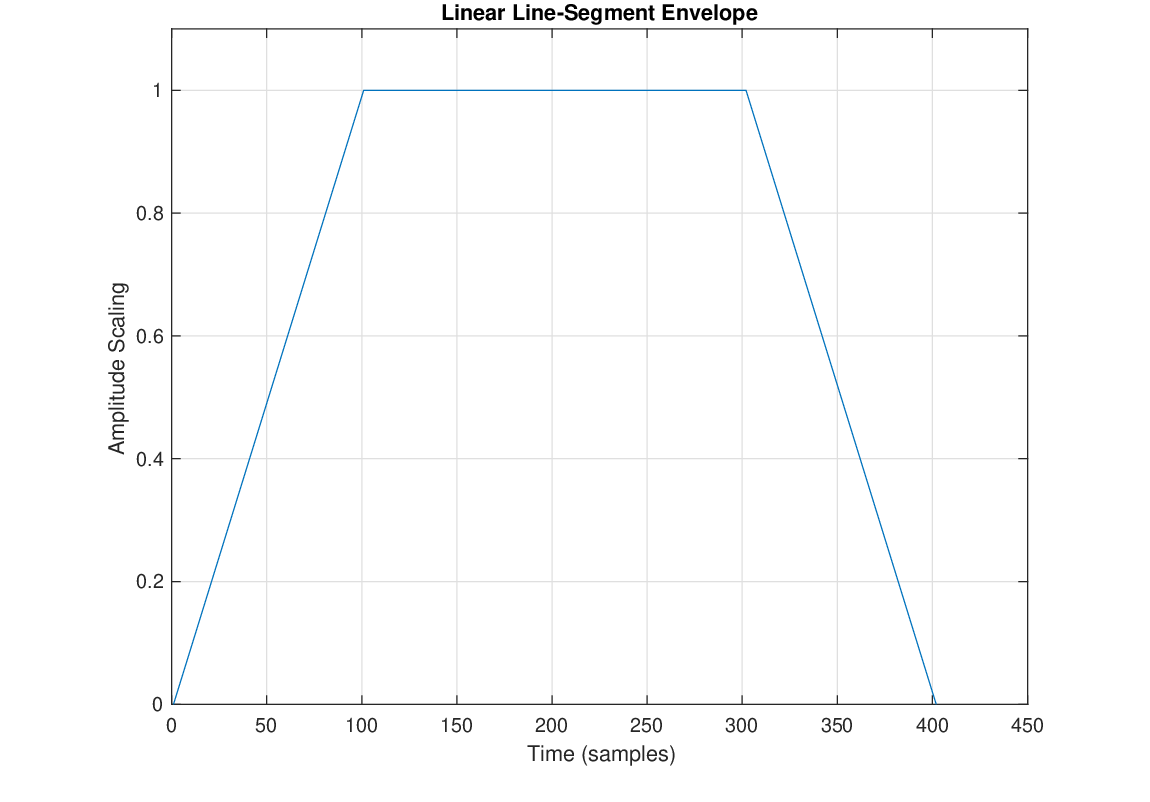
It is often necessary to map an audio parameter to a specific value range over a specific time duration. The most common example is to control the amplitude of a segment of an audio signal. For example, we typically want to smooth signal amplitudes over time, “ramping up” the gain of a chunk of sound when starting to listen to it and then “ramping down” the gain before we want to stop the sound. This is done to avoid discontinuities that might produce audible clicks or pops when being played through speakers. For this, we introduce the concept of time-dependent functions or envelopes that are typically designed to follow linear or exponential trajectories.
 is the slope of the line and
is the slope of the line and  is the point where the line crosses the vertical axis (
is the point where the line crosses the vertical axis (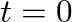 ).
).
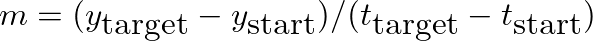 .
.
 ) at each time step:
) at each time step:
![$\displaystyle y[n] = m T_s + y[n-1],
$](img46.png)
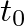 is the sampling period.
is the sampling period.
if ( atTarget == false ) {
if (target > value) {
value += rate;
if (value >= target) {
value = target;
atTarget = true;
}
}
else {
value -= rate;
if (value <= target) {
value = target;
atTarget = true;
}
}
}
return value;
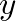
 is a scale factor calculated in a similar way to the linear line slope given above and
is a scale factor calculated in a similar way to the linear line slope given above and  is a curvature constant greater than zero.
is a curvature constant greater than zero.
 less than 1.0 produce "logarithmic" growth and exponential decay patterns. Values of
less than 1.0 produce "logarithmic" growth and exponential decay patterns. Values of  greater than 1.0 produce exponential growth and "logarithmic" decay patterns. A value of
greater than 1.0 produce exponential growth and "logarithmic" decay patterns. A value of  corresponds to linear growth and decay.
corresponds to linear growth and decay.
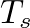 , remembering that exponential curves increase/decrease in equal proportion to their current value. This suggests an algorithm of the form:
, remembering that exponential curves increase/decrease in equal proportion to their current value. This suggests an algorithm of the form:
![$\displaystyle y[n] = a y[n-1] + (1-a) \mbox{target},
$](img52.png)
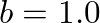 ,
, 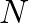 is the sample period, and
is the sample period, and 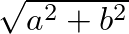 is a user provided time constant.
is a user provided time constant.

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |