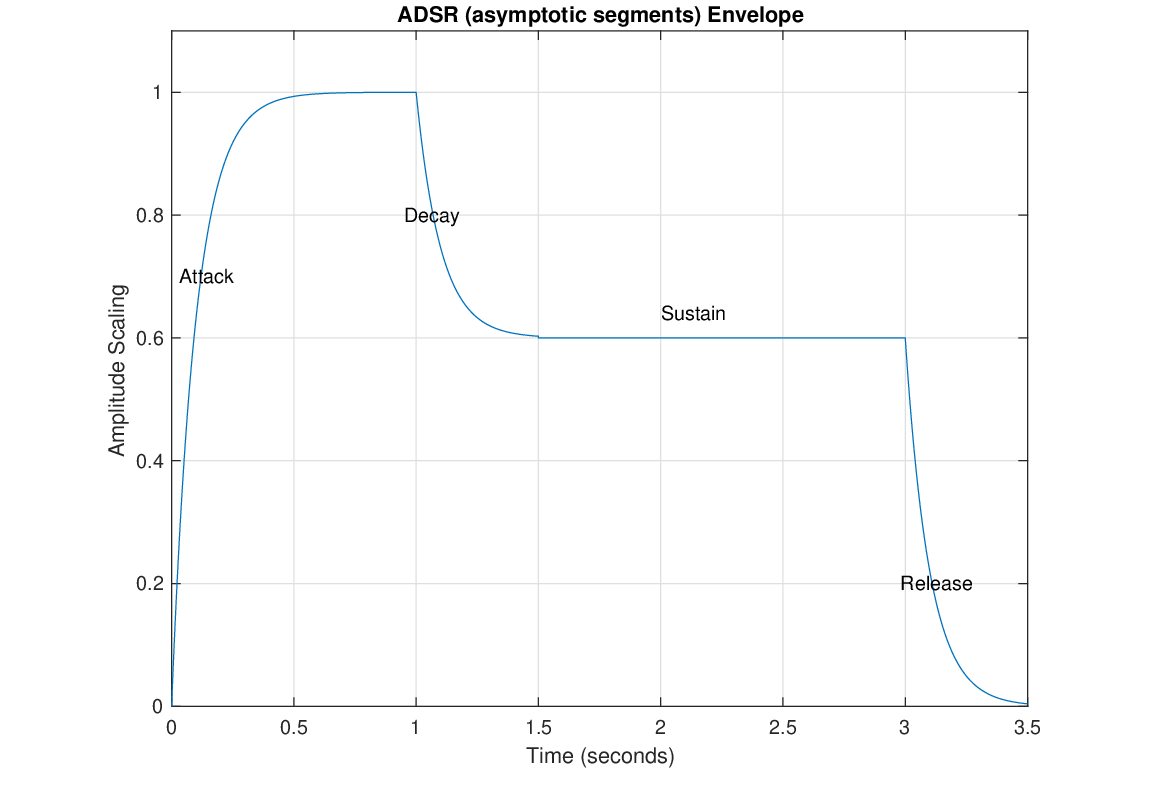
Next: Introduction to Pd Up: Discrete-Time Signals, Amplitude and Frequency Previous: Signal Amplitude Envelopes
 or 8. To lower a given pitch by three octaves, its frequency would be multiplied by
or 8. To lower a given pitch by three octaves, its frequency would be multiplied by  or 1/8.
or 1/8.
 .
.
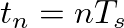 ) in Hertz is from a reference frequency (
) in Hertz is from a reference frequency (
 ), the following formula would be used:
), the following formula would be used:
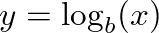
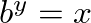
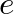 is the given MIDI note number.
is the given MIDI note number.
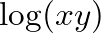
int n = (int) ( ( 12 * log(f / 220.0) / log(2.0) ) + 57.01 );

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |