Next: Forced Vibrations: Up: Lumped System Analysis: Previous: Lumped Elements:
In this section, we analyze the behaviour of particular combinations of masses, springs, and dashpots when given an initial displacement and/or velocity. We will consider forced oscillations in a subsequent section. The following linked online simulation provides useful visualizations for this section.
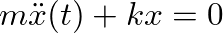
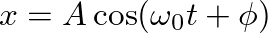 representing periodic motion.
representing periodic motion.
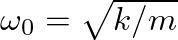 is the characteristic (or natural) angular frequency of the system.
is the characteristic (or natural) angular frequency of the system.
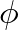 are determined by the initial displacement and velocity.
are determined by the initial displacement and velocity.
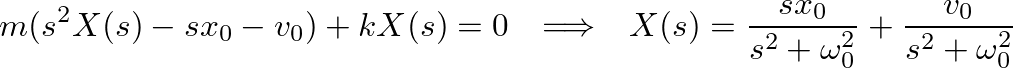
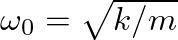 . From a table of Laplace transform pairs, the solution is found as:
. From a table of Laplace transform pairs, the solution is found as:
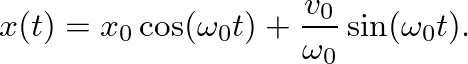
A physical system without losses is rare (if not impossible). The introduction of a mechanical dashpot in the mass-spring system provides damping and causes the resulting vibrations to decay over time.
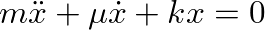
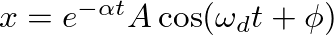 .
.
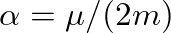 is a decay constant and
is a decay constant and
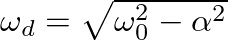 is the characteristic (or natural) angular frequency of the system.
is the characteristic (or natural) angular frequency of the system.
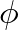 are determined by the initial displacement and velocity.
are determined by the initial displacement and velocity.
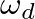 is lower than that of the mass-spring system (
is lower than that of the mass-spring system (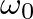 ).
).

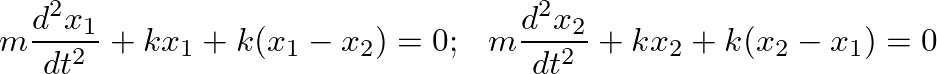
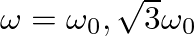 , where
, where
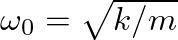

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |