Next: Sines + Noise: SMS Synthesis Up: Additive Synthesis Previous: Periodic Waveforms
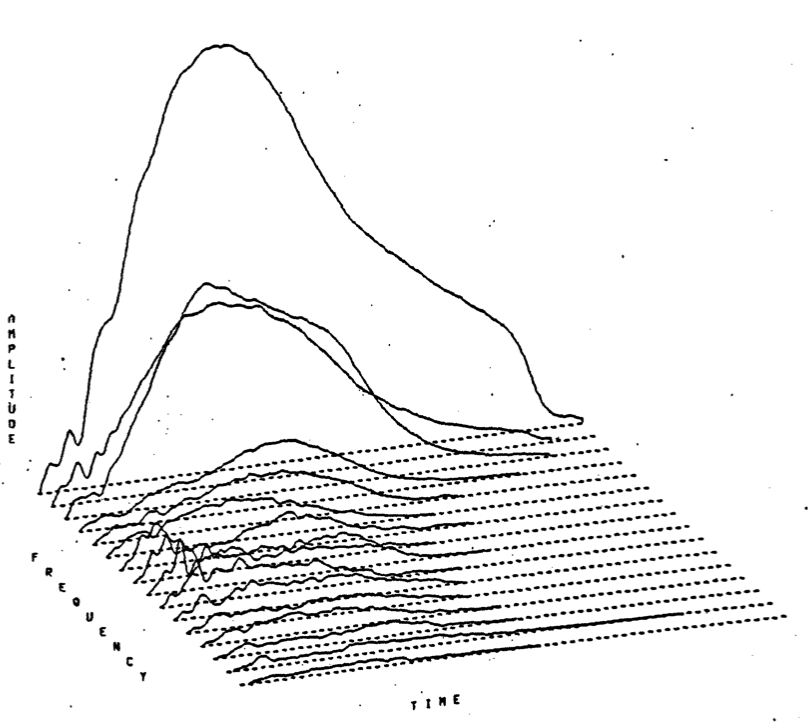
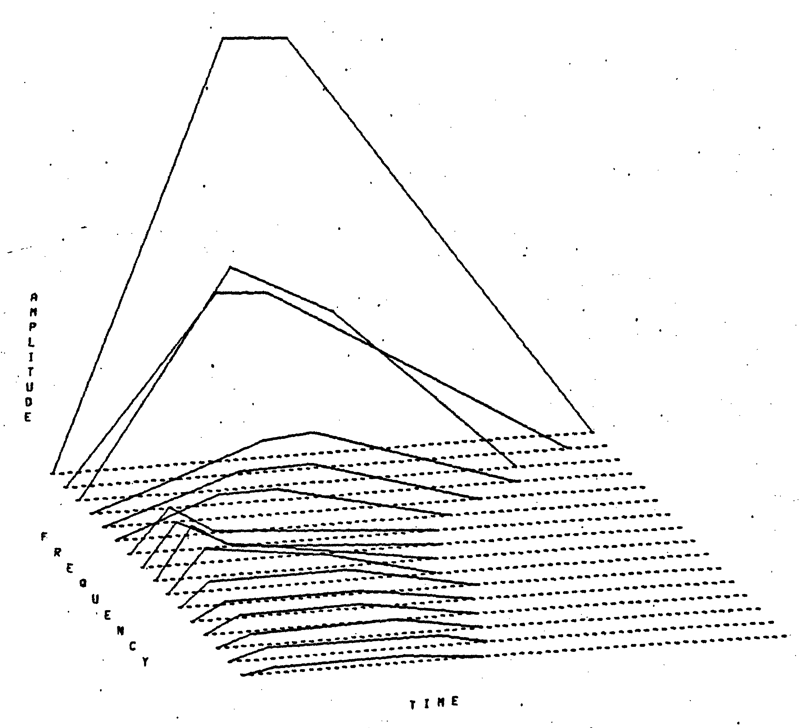
|
 and E
and E clarinets, the oboe, bassoon, tenor saxophone, trumpet, english horn, french horn and flute.
clarinets, the oboe, bassoon, tenor saxophone, trumpet, english horn, french horn and flute.

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |