Signals: Sampling and Aliasing

• Audio signals typically represent physical variables such as displacement, velocity, force, pressure, ...

• In most cases, we are concerned with variables that are time-dependent.

• A common signal used in audio processing and synthesis is a sinuoid, represented in continuous-time as:
  $$x(t) = A \sin(\omega t + \phi) = A \sin( 2 \pi f t + \phi),$$
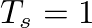
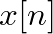  where $A$ is the peak amplitude, 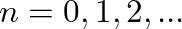$\omega = 2 \pi f$ is the radian frequency, 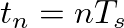$f$ is frequency in Hz, and 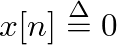$\phi$ is the initial phase of the sinusoidal signal.

• A sinusoid is the simplest example of a periodic signal. The period or duration of a single cycle of a periodic waveform is given by the inverse of its frequency $T = 1 / f$.

  Figure 1: A segment of a sinusoidal signal.

  

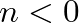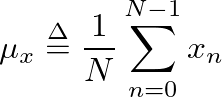• A discretized version of that same signal is found by making the substitution $t = n T_{s}$ in continuous-time expression, where 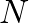$T_{s}$ is the sampling time interval or period and 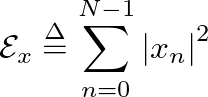$-\infty < n < \infty$ (integers). A sampled sinusoid will then have the form:
  $$x[n] = x(nT_{s}) = A \cos(\omega n T_{s} + \phi) = A \cos(\hat{\omega} n + \phi)$$
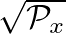  where $\hat{\omega} = \omega T_{s}$ is the normalized radian frequency.

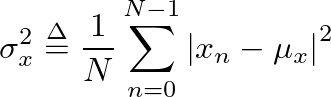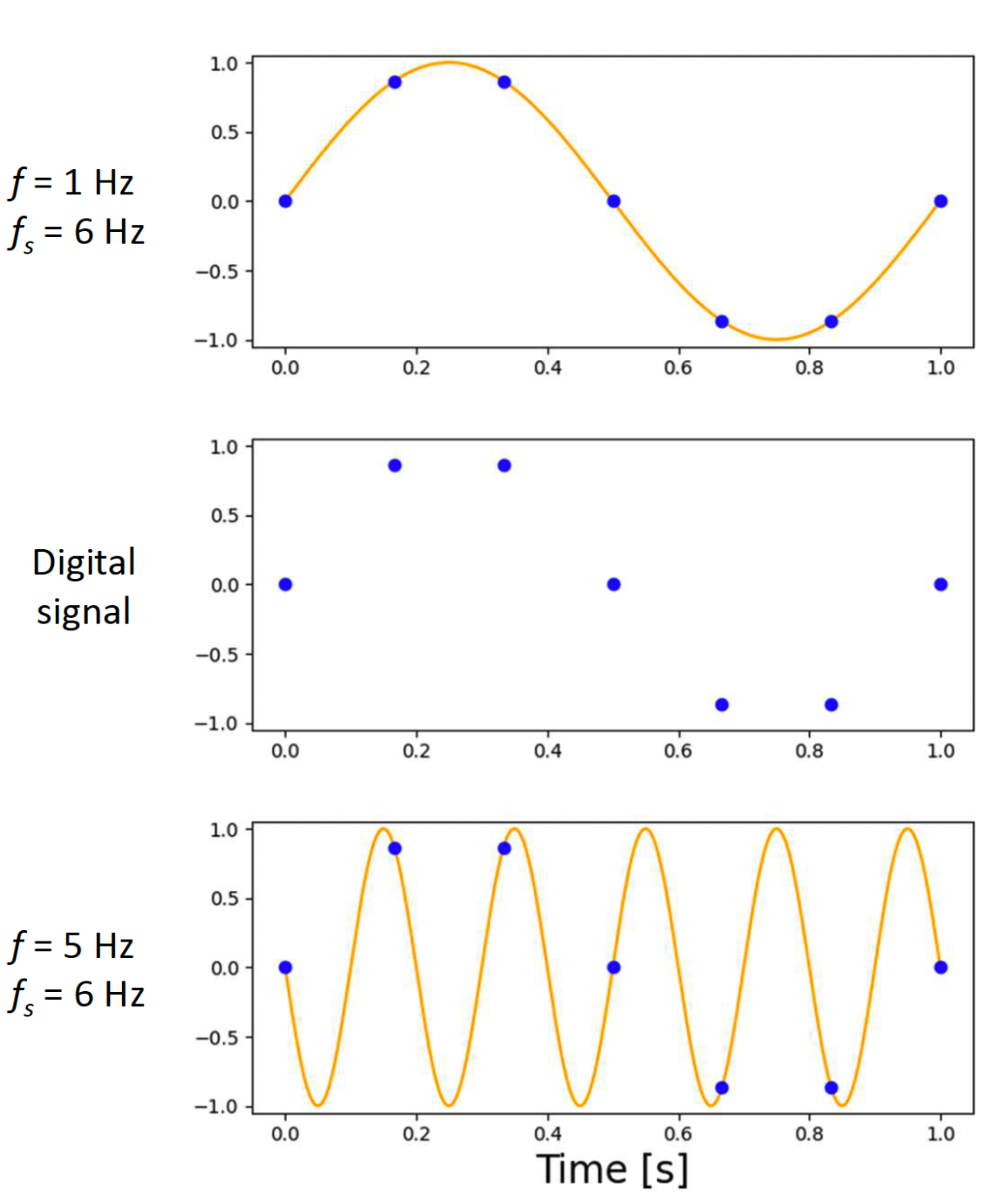
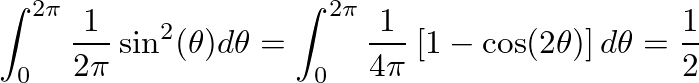• By Shannon's Sampling Theorem, a continuous-time signal $x(t)$ can be exactly reconstructed from its samples $x[n] = x(n T_{s})$ if the samples are taken at a rate $f_{s} = 1 / T_{s}$ that is greater than two times the highest frequency component in the signal.

• In other words, we must obtain more than two samples per period for all frequency components in a signal in order to accurately represent that signal.

• In order to satisfy this condition, signals are typically bandlimited or filtered before they are sampled (and after they are converted back to analog signals).

• If the sample rate does not meet the condition outlined above, any frequency components in the signal that are greater than $f_{s} / 2$ will “alias”.

• The Matlab script samplealiasing.m demonstrates aliasing.
  

• The recent trend toward very high sample rates (96 kHz, 182 kHz) is based more on hardware implementation issues than an attempt to accurately represent frequency components beyond the normal range of the human auditory system.

• It is worth noting that a sampling system must also have sufficient electrical headroom to capture the full amplitude range of a signal without “clipping.” Quantized amplitude levels can be mapped to different numerical formats (8-bit, 16-bit, 32-bit integers or floating-point numbers), which can have significant influence on the quality of a sampled signal.