Next: Reed Scattering Theory Up: Reed Valve Modeling Previous: Flow Through the Reed Orifice
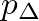 ) acting across it, Eq. (21) can be rewritten using Eq. (19) as
) acting across it, Eq. (21) can be rewritten using Eq. (19) as
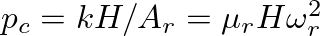 is the pressure necessary to push the reed against the mouthpiece facing and completely close the reed channel.
is the pressure necessary to push the reed against the mouthpiece facing and completely close the reed channel.
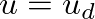 and we can use Eq. (22) and the relation
to find a set of solutions for various values of
and we can use Eq. (22) and the relation
to find a set of solutions for various values of 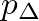 .
.
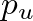 ) and obtain solutions for the outgoing downstream pressure
) and obtain solutions for the outgoing downstream pressure 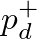 based on incoming pressures
based on incoming pressures 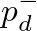 . This amounts to finding the intersection of the flow curve and a straight line corresponding to Eq. (23), as illustrated in Fig. 11 below.
. This amounts to finding the intersection of the flow curve and a straight line corresponding to Eq. (23), as illustrated in Fig. 11 below.
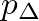 , which allows us to modify the mouth pressure in a time-domain simulation.
, which allows us to modify the mouth pressure in a time-domain simulation.
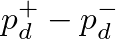 |
 |
![$\displaystyle p_{d}^{+} - p_{d}^{-} + [p_u - p_u] + [p_{d}^{-} - p_{d}^{-}]$](img102.png) |
|
 |
![$\displaystyle p_u - 2 p_{d}^{-} - p_u + [p_{d}^{+} + p_{d}^{-}]$](img103.png) |
||
 |
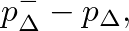 |
(24) |
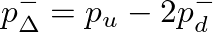 consists of pressure components known or computable from previous values.
consists of pressure components known or computable from previous values.
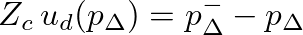 .
.
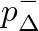 greater than
greater than 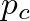 , the reed is closed and the solutions are given by a straight line of slope one, which corresponds to zero flow and pressure reflection without inversion at the junction.
, the reed is closed and the solutions are given by a straight line of slope one, which corresponds to zero flow and pressure reflection without inversion at the junction.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |