Next: Cylindrical Sections: Time-Domain Approach Up: Cylindrical Air Column Modeling Previous: Impulse Response
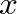 in a cylindrical pipe of finite length is given by
in a cylindrical pipe of finite length is given by
![$\displaystyle P(x,t) = \left[C^{+}e^{-jkx} + C^{-}e^{jkx}\right] e^{j\omega t},
$](img93.png) (37)
(37)
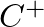 and
and 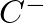 are complex traveling-wave amplitudes,
are complex traveling-wave amplitudes, 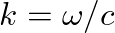 is the wave number,
is the wave number, 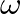 is radian frequency, and
is radian frequency, and 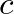 is the speed of sound in air.
is the speed of sound in air.
![$\displaystyle U(x,t) = \frac{1}{Z_{c}}\left[C^{+}e^{-jkx} - C^{-}e^{jkx}\right] e^{j\omega t},
$](img159.png) (38)
(38)
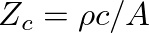 is the real-valued wave impedance of the pipe and
is the real-valued wave impedance of the pipe and 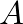 is its cross-sectional area.
is its cross-sectional area.
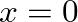 to
to 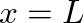 and is terminated at
and is terminated at 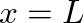 by the load impedance
by the load impedance 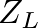 , it is possible to derive (from the equations above) an expression for the impedance at
, it is possible to derive (from the equations above) an expression for the impedance at 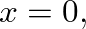 or the input impedance of the cylindrical pipe, given by
or the input impedance of the cylindrical pipe, given by
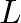 as
as
![$\displaystyle \left[\begin{array}{c} P_{0} \\ U_{0} \end{array}\right] = \left[...
...d \end{array}\right] \left[\begin{array}{c} P_{L} \\ U_{L} \end{array}\right],
$](img161.png) (41)
(41)
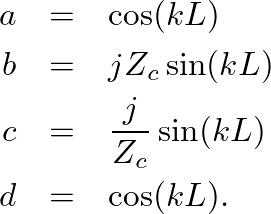
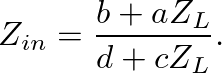 (42)
(42)
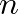 cylindrical sections, the input variables for each section become the output variables for the previous section. The transfer matrices can then be cascaded as
cylindrical sections, the input variables for each section become the output variables for the previous section. The transfer matrices can then be cascaded as
![$\displaystyle \left[\begin{array}{c} P_{0} \\ U_{0} \end{array}\right]$](img164.png) |
 |
![$\displaystyle \left[\begin{array}{cc} a_{1} & b_{1} \\ c_{1} & d_{1} \end{arra...
...n} \end{array}\right] \left[\begin{array}{c} P_{L} \\ U_{L} \end{array}\right]$](img165.png) |
|
 |
![$\displaystyle \left[\begin{array}{cc} A & B \\ C & D \end{array}\right] \left[\begin{array}{c} P_{L} \\ U_{L} \end{array}\right]$](img166.png) |
(43) |
![$\displaystyle \left[\begin{array}{cc} A & B \\ C & D \end{array}\right] = \prod...
...{n} \left[\begin{array}{cc} a_{i} & b_{i} \\ c_{i} & d_{i} \end{array}\right],
$](img167.png) (44)
(44)
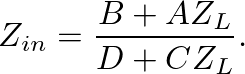 (45)
(45)
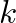 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |