Next: Cylindrical Air Column Modeling Up: Cylindrical Air Column Acoustics Previous: Cylindrical Pipes: Plane Wave Propagation
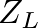 at one end of the tube will be partly reflected back into the tube and partly transmitted into the discontinuous medium.
at one end of the tube will be partly reflected back into the tube and partly transmitted into the discontinuous medium.
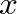 is given by
is given by
![$\displaystyle P(x,t) = \left[C^{+}e^{-jkx} + C^{-}e^{jkx}\right] e^{j\omega t},
$](img93.png) (22)
(22)
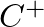 and
and 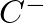 are complex amplitudes.
are complex amplitudes.
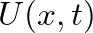 |
 |
![$\displaystyle \left(\frac{A}{\rho c}\right)\left[C^{+}e^{-jkx} - C^{-}e^{jkx}\right] e^{j\omega t}$](img98.png) |
|
 |
![$\displaystyle \frac{1}{Z_{c}}\left[C^{+}e^{-jkx} - C^{-}e^{jkx}\right] e^{j\omega t}$](img99.png) |
(23) |
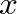 and time
and time 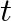 , the pressure and volume velocity traveling-wave components are related by
, the pressure and volume velocity traveling-wave components are related by
 (24)
(24)
 (25)
(25)
 superscripts indicate wave components traveling in the positive
superscripts indicate wave components traveling in the positive 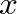 -direction or to the right, while negative
-direction or to the right, while negative 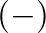 superscripts indicate travel in the negative
superscripts indicate travel in the negative 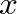 -direction or to the left.
-direction or to the left.
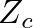 is a frequency-domain parameter, though for plane waves of sound it is purely real and independent of position. Therefore, these relationships are equally valid for both frequency- and time-domain analyses of pressure and volume velocity traveling-wave components.
is a frequency-domain parameter, though for plane waves of sound it is purely real and independent of position. Therefore, these relationships are equally valid for both frequency- and time-domain analyses of pressure and volume velocity traveling-wave components.
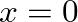 to
to 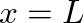 and is terminated at
and is terminated at 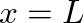 by the load impedance
by the load impedance 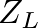 , the pressure wave reflectance is
and the transmittance is
, the pressure wave reflectance is
and the transmittance is
![$\displaystyle \frac{P(L,t)}{C^{+}} = e^{-jkL}\left[\frac{2 Z_{L}}{Z_{L} + Z_{c}}\right] e^{j\omega t}.
$](img108.png) (27)
(27)
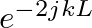 in Eq. (26) appears as a result of wave propagation from
in Eq. (26) appears as a result of wave propagation from 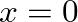 to
to 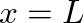 and back and has unity magnitude.
and back and has unity magnitude.
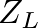 characterizes sound reflection and radiation at the end of the pipe.
characterizes sound reflection and radiation at the end of the pipe.
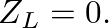 In this limit, the bracketed term of the reflectance becomes negative one, indicating that pressure traveling-wave components are reflected from the open end of a cylindrical tube with an inversion (or a
In this limit, the bracketed term of the reflectance becomes negative one, indicating that pressure traveling-wave components are reflected from the open end of a cylindrical tube with an inversion (or a  phase shift). There is no transmission of incident pressure into the new medium when
phase shift). There is no transmission of incident pressure into the new medium when 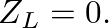
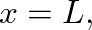 an appropriate load impedance approximation is
an appropriate load impedance approximation is
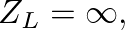 corresponding to
corresponding to 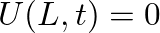 for all time. The bracketed term in Eq. (26) is then equal to one, which implies that pressure traveling waves reflect from a rigid barrier with no phase shift and no attenuation. The pressure “transmittance” (a bit of a misnomer in this case), has a magnitude of two at the rigid barrier.
for all time. The bracketed term in Eq. (26) is then equal to one, which implies that pressure traveling waves reflect from a rigid barrier with no phase shift and no attenuation. The pressure “transmittance” (a bit of a misnomer in this case), has a magnitude of two at the rigid barrier.
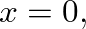 or the input impedance of the cylindrical tube, is given by
or the input impedance of the cylindrical tube, is given by
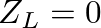 for an open end and
for an open end and
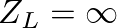 for a closed end. In this case, Equation (29) reduces to
for a closed end. In this case, Equation (29) reduces to
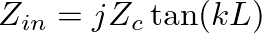 (30)
(30)
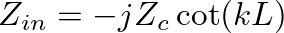 (31)
(31)
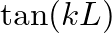 is approximated by
is approximated by 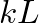 and the input impedance of the open pipe reduces to
and the input impedance of the open pipe reduces to
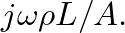 This is the expression for the impedance of a short open tube, or an acoustic inertance.
This is the expression for the impedance of a short open tube, or an acoustic inertance.
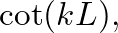 the input impedance of the rigidly terminated pipe reduces to
the input impedance of the rigidly terminated pipe reduces to
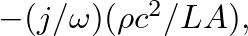 which is equivalent to the impedance of a cavity in the low-frequency limit.
which is equivalent to the impedance of a cavity in the low-frequency limit.
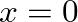 with a value of
with a value of 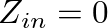 in the previous expressions, the resonance frequencies of the open-closed (o-c) pipe and the open-open (o-o) pipe are given for
in the previous expressions, the resonance frequencies of the open-closed (o-c) pipe and the open-open (o-o) pipe are given for
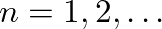 by
by

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |