Next: The Ideal Plucked String Up: String Modeling Previous: String Modeling
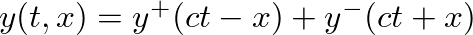 . If the string is fixed at
. If the string is fixed at 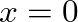 , then
, then 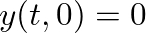 and
and
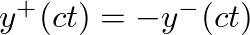 , which indicates that displacement traveling waves reflect from a fixed end with an inversion (or a reflection coefficient of -1).
, which indicates that displacement traveling waves reflect from a fixed end with an inversion (or a reflection coefficient of -1).
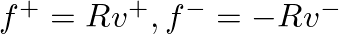 . At a rigid terminiation,
. At a rigid terminiation,
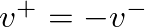 (from above). Thus, force wave components can be related at a rigid termination as:
(from above). Thus, force wave components can be related at a rigid termination as:
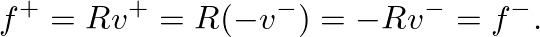
 because no transverse force is possible. At such a boundary, traveling-wave components of force must reflect with a coefficient of -1. To determine the reflection coefficient for displacement waves, we first note that force waves are proportional to the string slope. Differentiation of our general traveling-wave solution by
because no transverse force is possible. At such a boundary, traveling-wave components of force must reflect with a coefficient of -1. To determine the reflection coefficient for displacement waves, we first note that force waves are proportional to the string slope. Differentiation of our general traveling-wave solution by 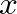 leads to (see this link):
leads to (see this link):
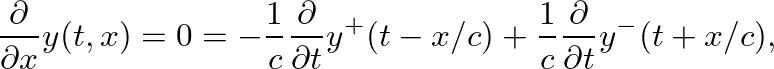
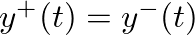 at
at 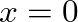 , indicating that displacement traveling waves reflect with a coefficient of +1.
, indicating that displacement traveling waves reflect with a coefficient of +1.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |