Next: Doppler Effect Up: Delay-Based Filters & Effects Previous: Flanging
![$\displaystyle y[n] = a_{2} x[n] + a_{1} x[n-1] + x[n-2] - a_{1} y[n-1] - a_{2} y[n-2],
$](img50.png)
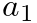 |
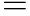 |
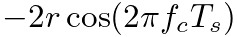 | ||
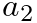 |
 |
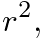 |
where 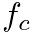 is the center frequency of the notch,
is the center frequency of the notch, 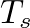 is the sample period, and
is the sample period, and 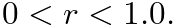 The closer
The closer 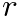 is to 1.0, the narrower the bandwidth of the notch.
is to 1.0, the narrower the bandwidth of the notch.
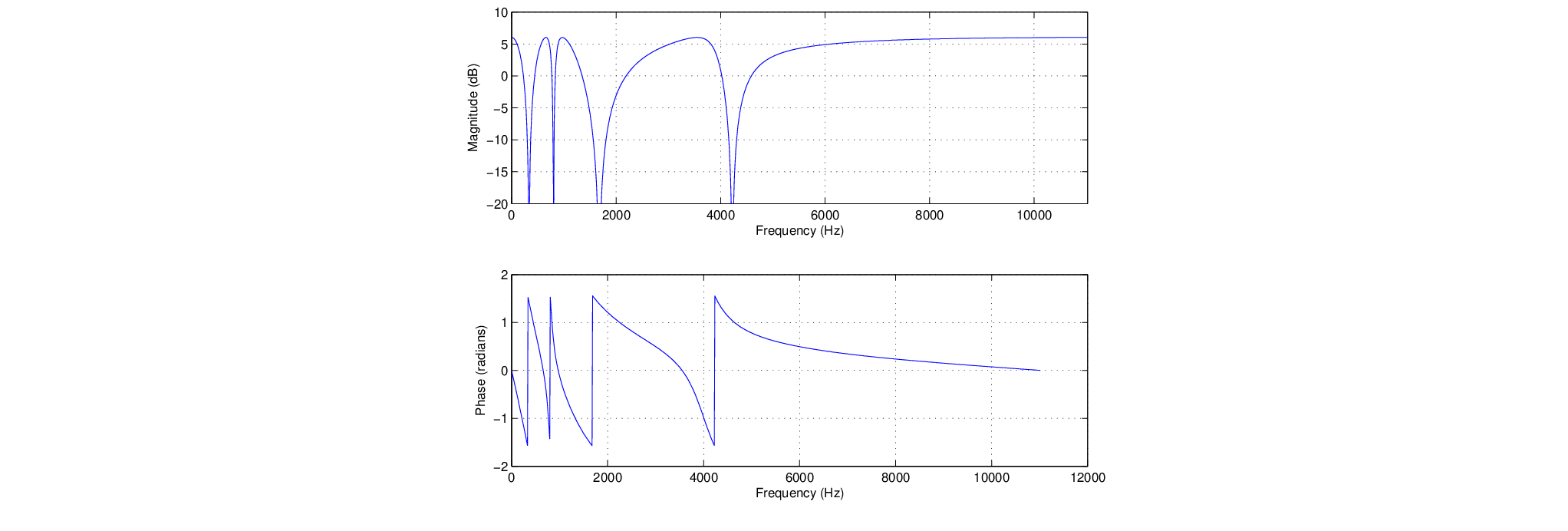
 (180 degrees). This happens close to the center frequencies of each allpass section.
(180 degrees). This happens close to the center frequencies of each allpass section.
 |
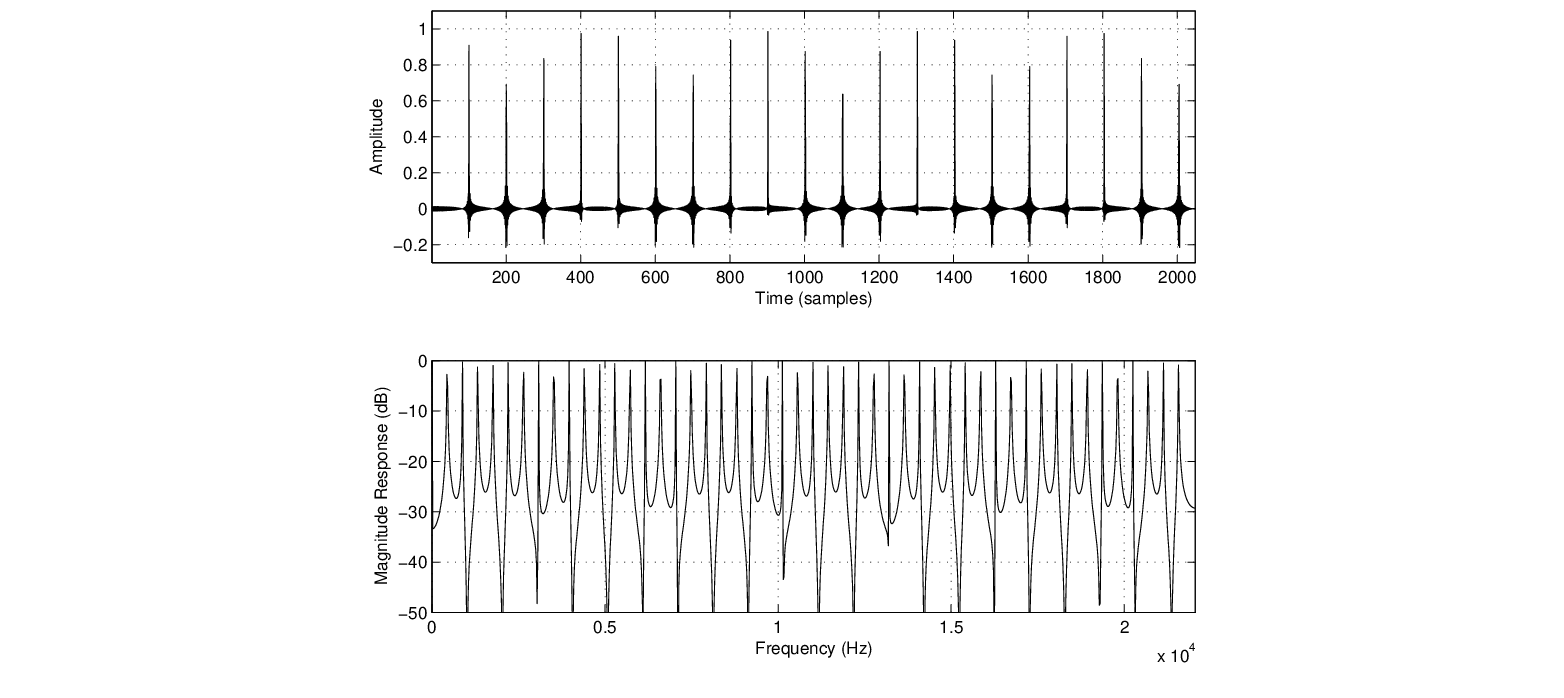 .
.

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |