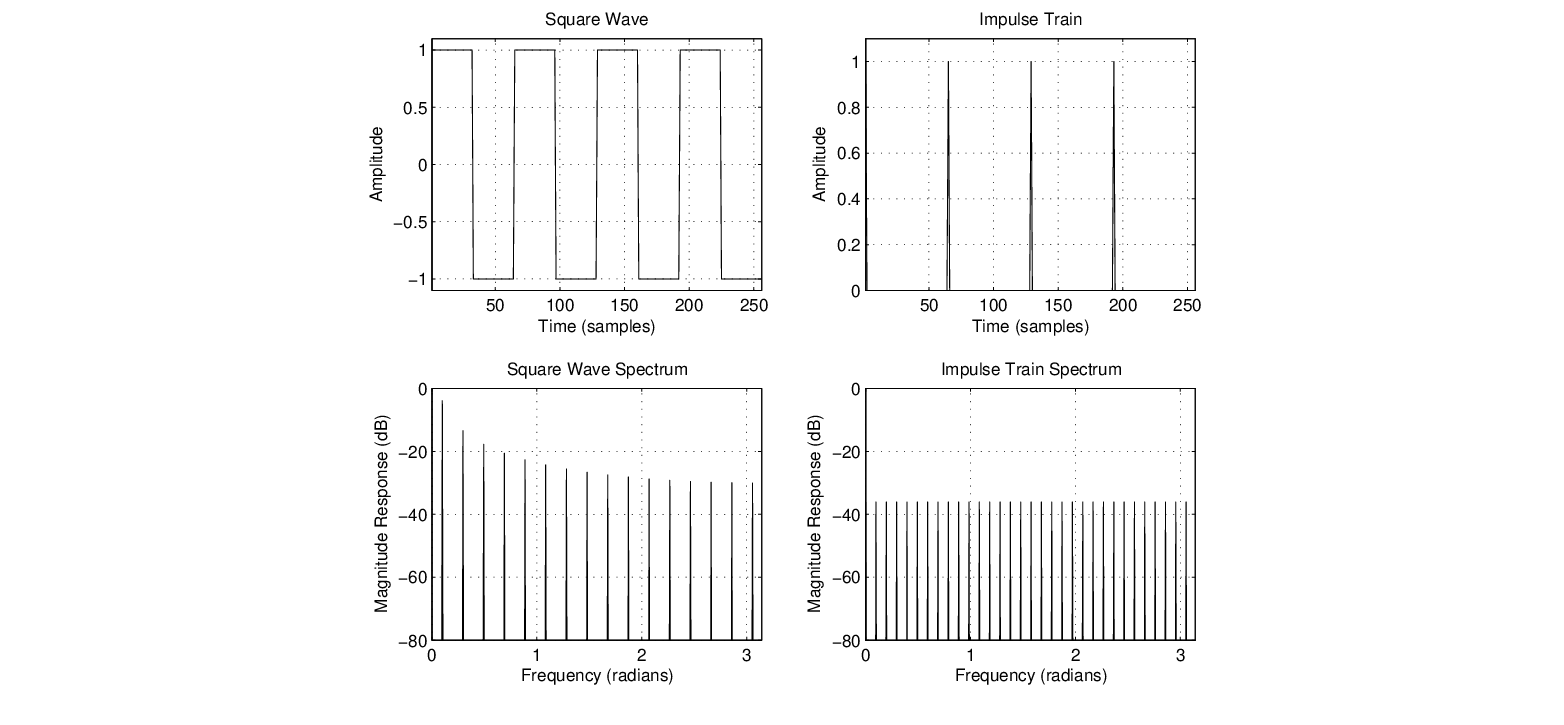
Next: Wave Reflections and “Echo” Up: Delay-Based Filters & Effects Previous: Delay-Based Filters & Effects
 between source and listener will result in a time delay of
between source and listener will result in a time delay of 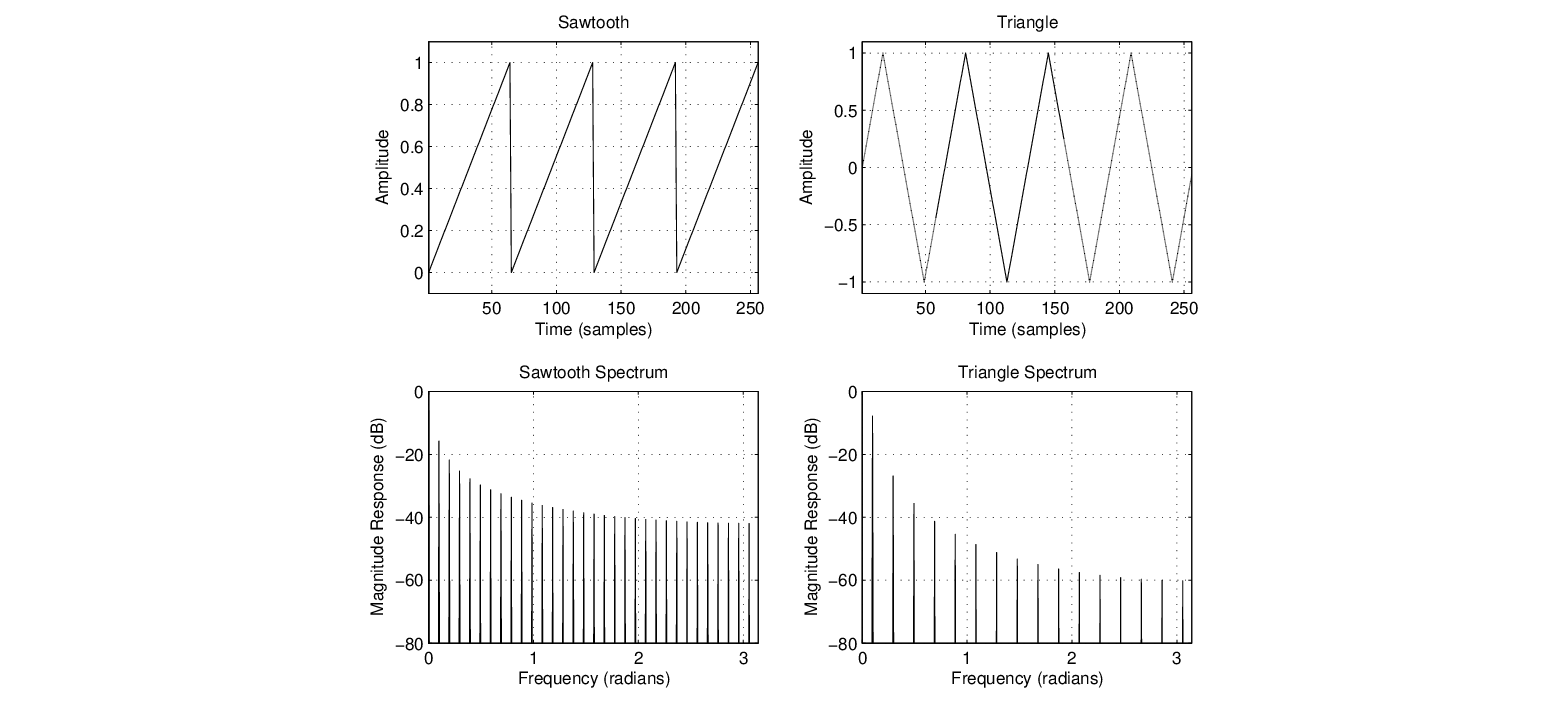 seconds (where
seconds (where 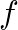 is the speed of sound propagation).
is the speed of sound propagation).
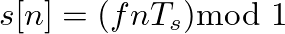 , where
, where 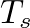 is the digital sample period (and
is the digital sample period (and  is the sampling rate in samples per second).
is the sampling rate in samples per second).
 represents the distance traveled by sound in a single sample period, which is about 7 millimeters at a sample rate of 48000 Hz.
represents the distance traveled by sound in a single sample period, which is about 7 millimeters at a sample rate of 48000 Hz.

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |