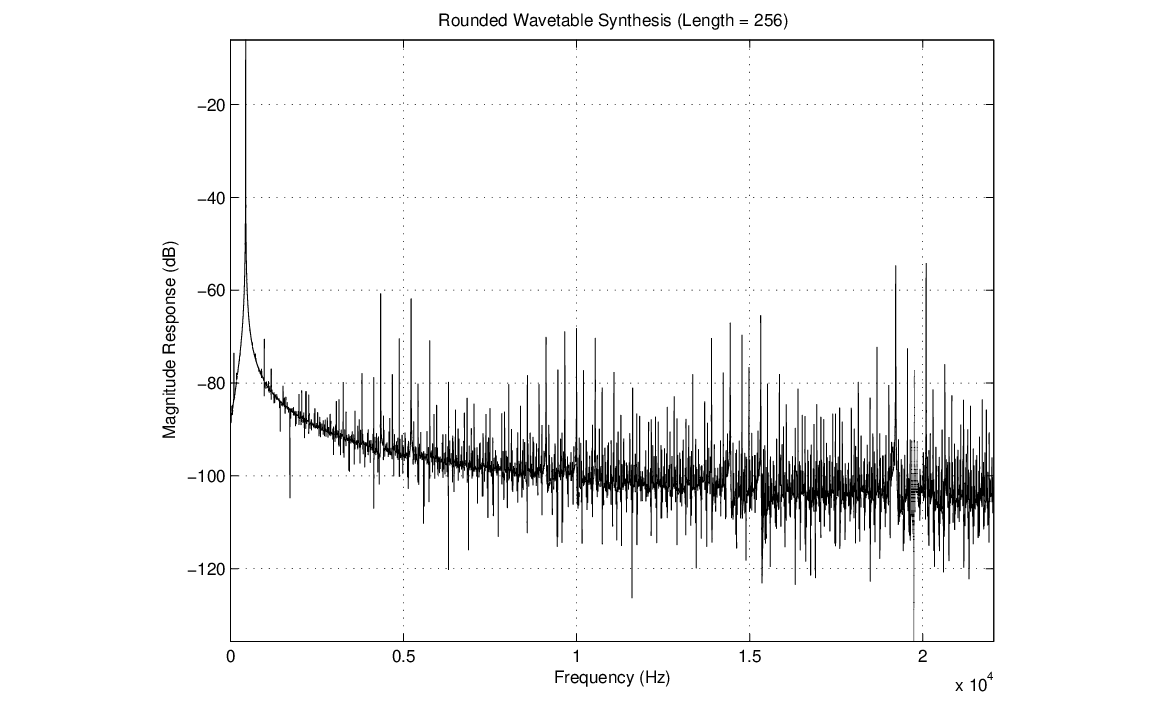
Next: Filtering in Pd Up: Digital Filtering Previous: Resonance Filters
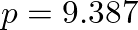 ,
,  , bandwidth, slope, ...
, bandwidth, slope, ...
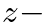 Transform.
Transform.
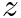 -Transform to Eq. 2,
-Transform to Eq. 2,

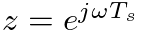 ,
,
 is in radians per second and
is in radians per second and 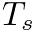 is the sample period.
is the sample period.
 , of the filter:
, of the filter:
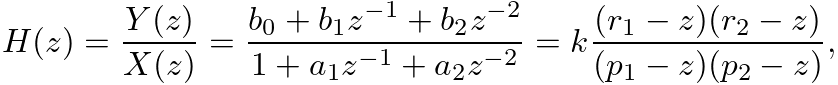
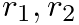 are complex roots of the numerator (called “zeros”) and
are complex roots of the numerator (called “zeros”) and  are complex roots of the denominator (called “poles”).
are complex roots of the denominator (called “poles”).

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |