Next: Resonance Filters Up: Digital Filtering Previous: Steady State and Transient Response
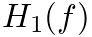 and
and 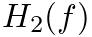 in Fig. 12 above would produce a new response given in the frequency domain by
in Fig. 12 above would produce a new response given in the frequency domain by 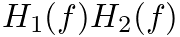 or in the time domain by
or in the time domain by
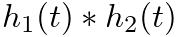 .
.
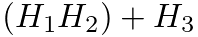 or time-domain response
or time-domain response
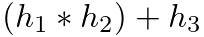 .
.
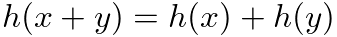 (mixing two tracks and filtering them is the same as filtering both tracks and mixing)
(mixing two tracks and filtering them is the same as filtering both tracks and mixing)
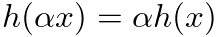 (you will get the same result if you amplify a track before or after filtering)
(you will get the same result if you amplify a track before or after filtering)
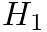 and
and  above without changing the result (
above without changing the result (
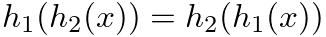 )
)

| ©2004-2025 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |