Time / Frequency Resolution

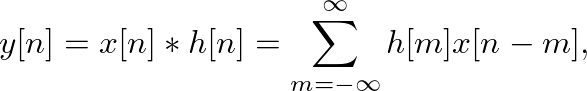• As mentioned above, a length $N$ FFT (or DFT) computes sinusoidal “weights” for 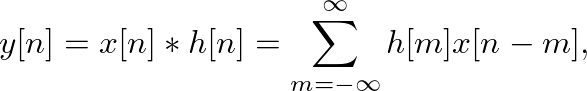$N$ evenly spaced frequencies between 0 and 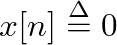$f_s (N-1)/N$. From the sampling theorem, only the first half of these frequency weights are unique.

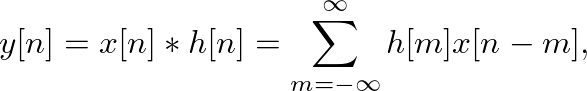• It follows that the larger the value of $N$, the more sinusoidal weights are computed and the smaller the spacing between frequency components. This spacing is given by $f_s/N$.

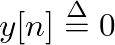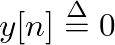• Note that this value ($f_s/N$) also represents the minimum non-zero frequency that can be resolved using a length 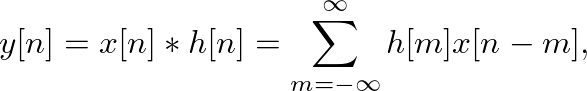$N$ DFT.

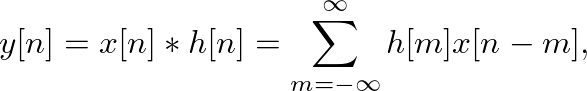• If analyzing a fairly static sound signal (that doesn't change over a long period of time), you would thus be best off using a larger value of $N$ to get a more precise estimate of the frequency content.

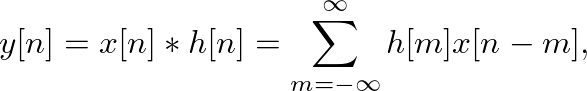• On the other hand, if the timbre of a sound changes significantly over time, you will need to segment the sound and compute separate FFTs over each block, in order to estimate the change of the frequency content from one block to another. This may require smaller values of $N$, in order to isolate changes over time.

• When computing FFTs over time (blocks), the resulting data can be displayed in terms of a waterfall plot (separate spectra slightly offset from one another) or as a spectrogram (a 2D time vs. frequency plot where spectral magnitudes are displayed using color maps).

  Figure 6: (Top Left) Spectrum plot over entire trumpet sound. (Top Right) A spectrogram plot of a trumpet sound. (Bottom) A waterfall plot of a trumpet sound.